Right Triangle With Side Lengths

When one angle is a 90-degree angle

A right triangle (American English language) or right-angled triangle (British), or more formally an orthogonal triangle , formerly called a rectangled triangle ^[1] (Ancient Greek: ὀρθόσγωνία, lit.'upright angle'),^[2] is a triangle in which one bending is a right bending (that is, a 90-degree angle), i.eastward., in which ii sides are perpendicular. The relation between the sides and other angles of the right triangle is the ground for trigonometry.

The side opposite to the right bending is called the hypotenuse (side c in the figure). The sides adjacent to the right angle are called legs (or catheti, singular: cathetus). Side a may exist identified as the side adjacent to bending B and opposed to (or opposite) bending A, while side b is the side next to angle A and opposed to angle B.

If the lengths of all three sides of a right triangle are integers, the triangle is said to be a Pythagorean triangle and its side lengths are collectively known as a Pythagorean triple.

Principal properties [edit]

Area [edit]

Equally with any triangle, the area is equal to one half the base multiplied past the corresponding height. In a right triangle, if one leg is taken as the base of operations then the other is meridian, and so the surface area of a correct triangle is one half the product of the 2 legs. Equally a formula the area T is

${\displaystyle T={\tfrac {i}{ii}}ab}$

where a and b are the legs of the triangle.

If the incircle is tangent to the hypotenuse AB at betoken P, and then denoting the semi-perimeter (a + b + c) / two every bit south, we have PA = s − a and Atomic number 82 = s − b , and the area is given by

${\displaystyle T={\text{PA}}\cdot {\text{Pb}}=(s-a)(due south-b).}$

This formula only applies to right triangles.^[three]

Altitudes [edit]

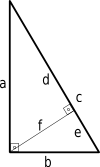
Altitude of a right triangle

If an altitude is drawn from the vertex with the correct angle to the hypotenuse then the triangle is divided into ii smaller triangles which are both similar to the original and therefore similar to each other. From this:

• The altitude to the hypotenuse is the geometric mean (mean proportional) of the two segments of the hypotenuse.^{[iv] : 243}
• Each leg of the triangle is the mean proportional of the hypotenuse and the segment of the hypotenuse that is adjacent to the leg.

In equations,

${\displaystyle \displaystyle f^{ii}=de,}$ (this is sometimes known as the right triangle altitude theorem)

${\displaystyle \displaystyle b^{2}=ce,}$

${\displaystyle \displaystyle a^{2}=cd}$

where a, b, c, d, e, f are as shown in the diagram.^[v] Thus

${\displaystyle f={\frac {ab}{c}}.}$

Moreover, the distance to the hypotenuse is related to the legs of the correct triangle past^{[6] [7]}

${\displaystyle {\frac {1}{a^{ii}}}+{\frac {1}{b^{2}}}={\frac {1}{f^{two}}}.}$

For solutions of this equation in integer values of a, b, f, and c, encounter here.

The distance from either leg coincides with the other leg. Since these intersect at the correct-angled vertex, the right triangle'southward orthocenter—the intersection of its iii altitudes—coincides with the right-angled vertex.

Pythagorean theorem [edit]

The Pythagorean theorem states that:

In any correct triangle, the expanse of the foursquare whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares whose sides are the two legs (the two sides that meet at a right angle).

This tin can be stated in equation form as

${\displaystyle \displaystyle a^{2}+b^{2}=c^{2}}$

where c is the length of the hypotenuse, and a and b are the lengths of the remaining two sides.

Pythagorean triples are integer values of a, b, c satisfying this equation.

Inradius and circumradius [edit]

Analogy of the Pythagorean Theorem

The radius of the incircle of a correct triangle with legs a and b and hypotenuse c is

${\displaystyle r={\frac {a+b-c}{2}}={\frac {ab}{a+b+c}}.}$

The radius of the circumcircle is half the length of the hypotenuse,

${\displaystyle R={\frac {c}{2}}.}$

Thus the sum of the circumradius and the inradius is half the sum of the legs:^[8]

${\displaystyle R+r={\frac {a+b}{ii}}.}$

I of the legs tin be expressed in terms of the inradius and the other leg as

${\displaystyle \displaystyle a={\frac {2r(b-r)}{b-2r}}.}$

Characterizations [edit]

A triangle ABC with sides ${\displaystyle a\leq b<c}$ , semiperimeter s, expanse T, altitude h opposite the longest side, circumradius R, inradius r, exradii r_a , r_b , r_c (tangent to a, b, c respectively), and medians 1000_a , one thousand_b , yard_c is a right triangle if and but if any one of the statements in the following half-dozen categories is truthful. All of them are of course also properties of a right triangle, since characterizations are equivalences.

Sides and semiperimeter [edit]

Angles [edit]

Area [edit]

Inradius and exradii [edit]

Altitude and medians [edit]

The altitude of a right triangle from its correct angle to its hypotenuse is the geometric mean of the lengths of the segments the hypotenuse is divide into. Using Pythagoras' theorem on the three triangles of sides (p +q, r, s ), (r, p, h ) and (s, h, q ),
${\displaystyle {\begin{aligned}(p+q)^{2}\;\;&=\quad r^{2}\;\;\,+\quad s^{ii}\\p^{2}\!\!+\!2pq\!+\!q^{2}&=\overbrace {p^{two}\!\!+\!h^{two}} +\overbrace {h^{2}\!\!+\!q^{2}} \\2pq\quad \;\;\;&=2h^{ii}\;\therefore h\!=\!{\sqrt {pq}}\\\stop{aligned}}}$

Circumcircle and incircle [edit]

Trigonometric ratios [edit]

The trigonometric functions for acute angles can exist defined as ratios of the sides of a right triangle. For a given angle, a right triangle may be constructed with this angle, and the sides labeled opposite, adjacent and hypotenuse with reference to this angle according to the definitions above. These ratios of the sides exercise not depend on the particular correct triangle chosen, but only on the given bending, since all triangles synthetic this fashion are similar. If, for a given angle α, the opposite side, adjacent side and hypotenuse are labeled O, A and H respectively, then the trigonometric functions are

${\displaystyle \sin \blastoff ={\frac {O}{H}},\,\cos \alpha ={\frac {A}{H}},\,\tan \alpha ={\frac {O}{A}},\,\sec \alpha ={\frac {H}{A}},\,\cot \alpha ={\frac {A}{O}},\,\csc \alpha ={\frac {H}{O}}.}$

For the expression of hyperbolic functions as ratio of the sides of a right triangle, encounter the hyperbolic triangle of a hyperbolic sector.

Special correct triangles [edit]

The values of the trigonometric functions can exist evaluated exactly for sure angles using correct triangles with special angles. These include the 30-threescore-90 triangle which can exist used to evaluate the trigonometric functions for whatsoever multiple of π/6, and the 45-45-90 triangle which can be used to evaluate the trigonometric functions for any multiple of π/4.

Kepler triangle [edit]

Let H, Grand, and A be the harmonic mean, the geometric hateful, and the arithmetic mean of two positive numbers a and b with a > b. If a right triangle has legs H and G and hypotenuse A, then^[15]

${\displaystyle {\frac {A}{H}}={\frac {A^{2}}{G^{ii}}}={\frac {G^{ii}}{H^{2}}}=\phi \,}$

and

${\displaystyle {\frac {a}{b}}=\phi ^{3},\,}$

where ${\displaystyle \phi }$ is the golden ratio ${\displaystyle {\tfrac {1+{\sqrt {5}}}{2}}.\,}$ Since the sides of this correct triangle are in geometric progression, this is the Kepler triangle.

Thales' theorem [edit]

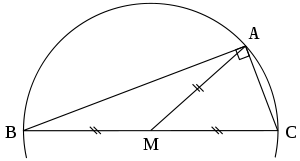
Median of a right angle of a triangle

Thales' theorem states that if A is any bespeak of the circle with diameter BC (except B or C themselves) ABC is a correct triangle where A is the right bending. The antipodal states that if a right triangle is inscribed in a circumvolve and so the hypotenuse will be a diameter of the circle. A corollary is that the length of the hypotenuse is twice the distance from the right angle vertex to the midpoint of the hypotenuse. As well, the center of the circle that circumscribes a right triangle is the midpoint of the hypotenuse and its radius is one half the length of the hypotenuse.

Medians [edit]

The following formulas concur for the medians of a right triangle:

${\displaystyle m_{a}^{2}+m_{b}^{2}=5m_{c}^{2}={\frac {5}{4}}c^{2}.}$

The median on the hypotenuse of a right triangle divides the triangle into two isosceles triangles, because the median equals one-one-half the hypotenuse.

The medians chiliad _a and m _b from the legs satisfy^{[eight] : p.136, #3110}

${\displaystyle 4c^{4}+9a^{2}b^{2}=16m_{a}^{ii}m_{b}^{two}.}$

Euler line [edit]

In a correct triangle, the Euler line contains the median on the hypotenuse—that is, it goes through both the right-angled vertex and the midpoint of the side opposite that vertex. This is because the right triangle'south orthocenter, the intersection of its altitudes, falls on the right-angled vertex while its circumcenter, the intersection of its perpendicular bisectors of sides, falls on the midpoint of the hypotenuse.

Inequalities [edit]

In any correct triangle the diameter of the incircle is less than half the hypotenuse, and more strongly information technology is less than or equal to the hypotenuse times ${\displaystyle ({\sqrt {2}}-ane).}$ ^{[16] : p.281}

In a correct triangle with legs a, b and hypotenuse c,

${\displaystyle c\geq {\frac {\sqrt {ii}}{2}}(a+b)}$

with equality just in the isosceles instance.^{[16] : p.282, p.358}

If the altitude from the hypotenuse is denoted h _c , and so

${\displaystyle h_{c}\leq {\frac {\sqrt {2}}{iv}}(a+b)}$

with equality just in the isosceles example.^{[sixteen] : p.282}

Other backdrop [edit]

If segments of lengths p and q emanating from vertex C trisect the hypotenuse into segments of length c/iii, then^{[4] : pp. 216–217}

${\displaystyle p^{2}+q^{2}=five\left({\frac {c}{three}}\right)^{two}.}$

The right triangle is the only triangle having two, rather than one or 3, distinct inscribed squares.^[17]

Given h > k. Let h and k be the sides of the two inscribed squares in a right triangle with hypotenuse c. So

${\displaystyle {\frac {ane}{c^{2}}}+{\frac {i}{h^{two}}}={\frac {1}{k^{two}}}.}$

These sides and the incircle radius r are related by a similar formula:

${\displaystyle \displaystyle {\frac {1}{r}}=-{\frac {1}{c}}+{\frac {one}{h}}+{\frac {1}{chiliad}}.}$

The perimeter of a correct triangle equals the sum of the radii of the incircle and the 3 excircles:

${\displaystyle a+b+c=r+r_{a}+r_{b}+r_{c}.}$

See as well [edit]

• Astute and obtuse triangles (oblique triangles)
• Screw of Theodorus

References [edit]

1. ^ Howard, G.Due south.; Bettesworth, J.; Boswell, H.; Stonehouse, F.; Hogg, A. (1788). THE NEW ROYAL CYCLOPAEDIA... Retrieved 2022-03-07 .
2. ^ Daniel Parrochia (24 July 2018). Mathematics and Philosophy. John Wiley & Sons. pp. 72–. ISBN978-i-78630-209-0.
3. ^ Di Domenico, Angelo S., "A property of triangles involving expanse", Mathematical Gazette 87, July 2003, pp. 323-324.
4. ^ ^{a b} Posamentier, Alfred S., and Salkind, Charles T. Challenging Problems in Geometry, Dover, 1996.
5. ^ Wentworth p. 156
6. ^ Voles, Roger, "Integer solutions of ${\displaystyle a^{-2}+b^{-2}=d^{-2}}$ ," Mathematical Gazette 83, July 1999, 269–271.
7. ^ Richinick, Jennifer, "The upside-downwards Pythagorean Theorem," Mathematical Gazette 92, July 2008, 313–317.
8. ^ ^{a b c d eastward} Inequalities proposed in "Crux Mathematicorum", [one].
9. ^ "Triangle right iff southward = 2R + r, Art of problem solving, 2011". Archived from the original on 2014-04-28. Retrieved 2012-01-02 .
10. ^ ^{a b c d} Andreescu, Titu and Andrica, Dorian, "Complex Numbers from A to...Z", Birkhäuser, 2006, pp. 109-110.
11. ^ "Properties of Right Triangles". Archived from the original on 2011-12-31. Retrieved 2012-02-15 .
12. ^ ^{a b c} CTK Wiki Math, A Variant of the Pythagorean Theorem, 2011, [two] Archived 2013-08-05 at the Wayback Auto.
13. ^ Darvasi, Gyula (March 2005), "Converse of a Belongings of Right Triangles", The Mathematical Gazette, 89 (514): 72–76, doi:10.1017/S0025557200176806, S2CID 125992270 .
14. ^ Bell, Amy (2006), "Hansen'south Correct Triangle Theorem, Its Antipodal and a Generalization" (PDF), Forum Geometricorum, 6: 335–342
15. ^ Di Domenico, A., "The golden ratio — the right triangle — and the arithmetic, geometric, and harmonic ways," Mathematical Gazette 89, July 2005, 261. Also Mitchell, Douglas Westward., "Feedback on 89.41", vol 90, March 2006, 153-154.
16. ^ ^{a b c} Posamentier, Alfred S., and Lehmann, Ingmar. The Secrets of Triangles. Prometheus Books, 2012.
17. ^ Bailey, Herbert, and DeTemple, Duane, "Squares inscribed in angles and triangles", Mathematics Mag 71(4), 1998, 278-284.

• Weisstein, Eric West. "Right Triangle". MathWorld.
• Wentworth, G.A. (1895). A Text-Volume of Geometry. Ginn & Co.

External links [edit]

• Reckoner for right triangles Archived 2017-09-30 at the Wayback Motorcar
• Advanced correct triangle calculator

Right Triangle With Side Lengths,

Source: https://en.wikipedia.org/wiki/Right_triangle

Posted by: gallardothercits.blogspot.com

Share this post